Rolles is a special case, where the endpoints have the same y coordinate, so the tangent and chord are horizontal. F(x) = x^3 − x^2 − 20x + 6, 0, 5 f(0)= 6; f(5)= 125-25-100+6= 6. So Rolles thm applies: for (0,6) and (5,6) there must be a value,c, between 0 and 5, where the slope is zero. Y' = 3x^2 -2x -20= 0. View 5.2SkillBuilder.pdf from MATH 122 at University of Mary Washington. Avon High School Name AP Calculus AB Period Score / 10 Skill Builder: Topic 5.2 – Extreme Value Theorem; Global vs.

Case 2: The function is not constant.

Since the function isn't constant, it must change directions in order to start and end at the same $$y$$-value. This means somewhere inside the interval the function will either have a minimum (left-hand graph), a maximum (middle graph) or both (right-hand graph).

So, now we need to show that at this interior extrema the derivative must equal zero. The rest of the discussion will focus on the cases where the interior extrema is a maximum, but the discussion for a minimum is largely the same.

Possibility 1: Could the maximum occur at a point where $$f'>0$$?

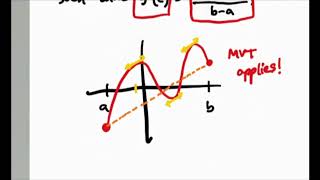
5.2 Rolle's Theorem & Mvtap Calculus Equation

No, because if $$f'>0$$ we know the function is increasing. But it can't increase since we are at its maximum point.

5.2 Rolle's Theorem Equation

Possibility 2: Could the maximum occur at a point where $$f'<0$$?

5.2 Rolle's Theorem & Mvtap Calculus Solver

No, because if $$f'<0$$ we know that function is decreasing, which means it was larger just a little to the left of where we are now. But we are at the function's maximum value, so it couldn't have been larger.

Rolle's Theorem Proof

Since $$f'$$ exists, but isn't larger than zero, and isn't smaller than zero, the only possibility that remains is that $$f' = 0$$.

And that's it! We showed that the function must have an extrema, and that at the extrema the derivative must equal zero!